Il modo in cui noi immaginiamo essere strutturata la musica sicuramente influenza quello in cui componiamo, improvvisiamo e più in generale la percepiamo.
Il fatto che la musica occidentale si sia sviluppata a partire dal XVII secolo intorno al concetto di tonalità ha influenzato in modo tanto profondo la nostra cultura da far si che tuttora, nonostante un XX secolo ricco di sperimentazioni, consideriamo la musica costruita intorno a questo principio come la più immediata, semplice e facilmente percepibile.
Che ci debba quindi essere una nota predominante, fondamentale, e che su questa si possa sviluppare in direzione verticale verso l’alto un’armonia che possa poi avere un ulteriore sviluppo orizzontale determina una prassi compositiva e una forma della musica ben determinata nella sua visione spaziale e nella sua distribuzione delle altezze.
Che si possano creare e utilizzare sistemi alternativi per creare geometrie armoniche e melodiche e che questi possano essere validi e fertili da un punto di vista creativo ed espressivo è ormai un dato consolidato della musica contemporanea.
Una visione geometrica della composizione musicale non è un accessorio intellettuale della musica di ricerca occidentale, infatti in molte musiche extra europee o nella musica antica l’elemento geometrico, numerico e astratto è fondamentale e talvolta fondante.
L’idea della presenza di una nota fondamentale trova comunque fondamento nella costituzione fisico-acustica di un’onda sonora e risponde quindi a un’esperienza percettiva concreta lì dove ogni suono è composto da un’onda fondamentale e da una serie di armonici superiori di inferiore intensità.
Si può però utilizzare l’idea della predominanza di una certa altezza sulle altre in diversi modi. Ad es. considerando una nota come asse di riferimento intorno al quale si può sviluppare il materiale in direzione verticale sia verso l’alto che verso il basso, secondo un principio di simmetria, rispetto al solo sviluppo verso l’alto della musica tonale.
Un artista che ha sviluppato in modo originale e organico questo concetto è il sassofonista Steve Coleman. Intorno a questa intuizione, che ha comunque radici lontane anche nella musica europea, ha elaborato una personale idea dello sviluppo melodico e armonico, che si riflette sia nelle composizioni che nelle improvvisazioni.
http://m-base.com/essays/symmetrical-movement-concept/
Un altro concetto interessante e argomentato in modo originale da parte di Coleman è quello del movimento del materiale melodico improvvisativo. Le linee disegnate dal fraseggio del grande sassofonista Charlie Parker, soprannominato non a caso Bird, vengono paragonate a quelle di un uccello in volo. Coleman, partendo da questa analogia, sostiene di essersi ispirato invece al volo irrequieto e rapido delle api.
Negli ultimi anni ho avuto modo di sperimentare l’utilizzo nell’improvvisazione di un numero limitato di intervalli.
Ogni intervallo ha determinate proprietà e si rapporta con l’insieme cromatico in modo peculiare: la quarta aumentata lo divide in due sezioni perfettamente simmetriche, il tono in sei, la terza minore in quattro, la terza maggiore in tre, la quarta e il semitono in dodici.
Gli intervalli complementari, quinta, sesta e settima godono delle stesse proprietà dei loro reciproci.
Ne deriva che il semitono, la settima maggiore, la quarta e la quinta sono intervalli estremamente fluidi e dinamici, mentre la quarta aumentata è l’intervallo più statico. Non mi riferisco qui alla caratteristica timbrica dell’intervallo, il cui colore è qualcosa di diverso, e il cui effetto alle volte non può essere considerato a prescindere del contesto armonico in cui viene utilizzato, ma alla capacità dinamica dello stesso rispetto al totale cromatico.
Se è facile valutare lo sviluppo di un singolo intervallo la faccenda diventa più complessa quando si considerano le combinazioni tra due intervalli, alternati in modo regolare. Il totale delle combinazioni possibili è 30, sempre considerando gli intervalli dalla quinta alla settima riconducibili ai loro complementari di ampiezza inferiore.
Due intervalli che si alternano in modo equilibrato in direzione verticale generano una successione che è determinata dalla somma dei due. Una seconda minore alternata a una maggiore ad es. genera una terza minore, creando una progressione a terze minori che divide l’ottava in quattro parti uguali, generando una scala ottofonica diminuita.
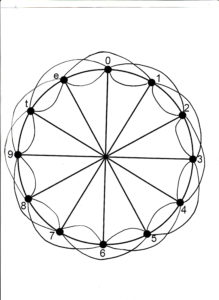
Diverso e interessante è il processo nel caso in cui due intervalli siano alternati invertendo la direzione a ogni coppia di note. Si genera in questo modo un movimento circolare che riporta sempre al punto di partenza, anzi se lo visualizziamo graficamente il movimento è una sorta di strano anello, quasi un nodo (fig. 1).
Possiamo considerare i nostri intervalli come due vettori bidimensionali il cui valore è determinato dall’ampiezza dell’intervallo e dalla direzione verso l’alto o il basso.
In matematica il vettore è un elemento quantitativo (l’intervallo) che possiede un verso direzionale (alto o basso), in questo caso monodimensionale visto che un’altezza può muoversi solo lungo un asse.
Dei due intervalli il primo (le note c-d nella fig. 1) possiamo definirlo vettore caratterizzante e il secondo (d-c# fig. 1) vettore traspositore. Con il primo infatti stabiliamo il primo passo, la lunghezza del nostro primo anello, con il secondo stabiliamo la distanza con la quale trasportiamo questo intervallo. Completando il nostro processo con una seconda maggiore verso il basso (c#-b) e una seconda minore verso l’alto (b-c) completiamo il nostro primo ciclo.
Il processo essendo perfettamente equilibrato dal punto di vista degli intervalli (i vettori si annullano) riconduce in modo circolare la frase al punto iniziale.
Possiamo fare un ulteriore passo considerando come sviluppare questa idea circolare.
La prima frase vedeva la successione di un vettore positivo, due negativi e uno positivo. Ora possiamo modificare questa sequenza con due vettori positivi e due successivi negativi.
Le due cellule in sequenza generano il frammento della fig. 2, dove è interessante osservare che le due cellule hanno in comune le prime due note, ovvero il primo intervallo caratterizzante, che diviene l’asse di equilibrio della nostra frase.
Estendendo questo processo spostandosi di un intervallo traspositore, vista l’alternanza degli intervalli, si otterranno una serie di frasi circolari inanellate le une con le altre. Interessante osservare che ogni doppio anello si trasla verso l’alto con una proporzione che è il doppio del valore del vettore traspositore.
In questo caso il risultato sarà un tono, generando quindi complessivamente una progressione a toni interi (fig. 3).
Nella discesa il processo si inverte. La successione dei vettori sarà positiva, negativa, negativa, positiva. A questo succederà una successione positiva, positiva, negativa, negativa. In questo modo l’asse si sposta dal primo intervallo caratterizzante al secondo.
Questa frase ha quindi la proprietà di alternare in modo circolare tono e semitono, con una progressione di toni interi ascendenti e discendenti.
Ora possiamo osservare la nostra successione di intervalli dal punto di vista delle classi di insiemi che esprime.
Nel mio precedente articolo ho analizzato per sommi capi la metodologia che consente di estrapolare questi valori: http://www.nicolafazzini.com/wp/?p=158
Il primo anello è riconducibile all’insieme 4-1 (0,1,2,3) [3,2,1,0,0,0].
Con l’aggiunta del secondo si ottiene l’insieme 5-1 (0,1,2,3,4) [4,3,2,1,0,0].
Questa successione di anelli tono/semitono esprime una progressione di toni, ma nella sua natura intervallare esprime un’evidente prevalenza dell’intervallo di semitono. Interessante osservare una curiosa analogia dove il codice che esprime la successione delle altezze è speculare a quello degli intervalli contenuti.
Questo fraseggio è per me particolarmente interessante proprio per la sua capacità circolare e la possibilità di legare gli intervalli in modo fluido e invertire la direzione delle frasi mantenendo un equilibrio tra sviluppo orizzontale e verticale dell’improvvisazione.
Se qualcuno trova che questo sia troppo matematico o astratto, provi a suonare la frase per intero e a sviluppare questa idea utilizzando altri intervalli e si ricrederà!
Bibliografia e Link:
Persichetti Vincent, Guerini Scientifica (2009) – Armonia del ventesimo secolo
Levy Ernst, Sigmund Lavarie (1985) – A Theory of Harmony
http://m-base.com/essays/symmetrical-movement-concept/